Pinhole Images and Their Quality

A pinhole doesn't just pass light through it in proportion the to its area A = πr². There are other effects such as scattering off the sides of the pinhole and diffraction which may be considered proportional to its perimeter P = 2πr, with r being the pinhole radius. The relative flux for the two effects is proportional to the ratio P/A = (2πr)/(πr²) = 2/r which tells us that the perimeter effects dominate for small r. If the pinhole is large enough we can ignore the perimeter effects since the cross-sectional area of a hole increases more rapidly than its perimeter.

For a section of the pinhole image of area dA_i the pinhole acts as an optical stop which blocks some of the light from sections of the illuminating object but allows other sections such as area dA_o to pass through. The light reaching a point on the screen is the sum of the areas passing through and one can apply the laws of photometry to determine the illuminance of a portion of the image.


The quality of the image depends on the relative angular size of the pinhole at the image point and if the distance of the screen, d, is much larger than the radius of the pinhole the angular size is approximately θ = 2r/d. One has to compare this value with the angular size of an actual object in the field of view to determine how detailed its image will be.

Supplemental (Mar 24): I did a plot of the number of pixels for an image of the Sun:


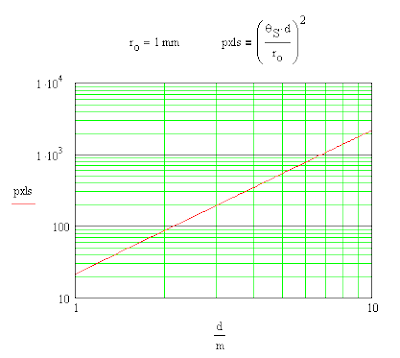
One can see that r_o/d severely limits the image resolution for a pinhole camera.