The Almagest tells us that Ptolemy had access to the works of Hipparchus, Aristarchus of Samos, Timocharis, and Aristillus who probably all worked for the Musaeum of Alexandria at one time and its companion institution the Library of Alexandria. One of the functions of the Musaeum was that of an astronomical institute. Ptolemy had access to, studied and added to these records and the result was the Almagest. But precisely where did Ptolemy work?
The Library of Alexandria was distroyed 48 BC in when the Romans invaded Egypt. It is claimed that the neighboring Musaeum survived. When Mark Anthony later ruled in Egypt he presented the Library of Pergamon to Cleopatra as a gift. The remnants of the Library were moved to the vicinity of the Serapeum, a temple dedicated to the Greek/Egyptian god Serapis.
The century after Ptolemy's time we know that the Brucheion, the Royal Quarter in Alexandria, was distroyed by Aurelian. It is debatable whether or not the Musaeum still existed at this time. It is possible that some of the scholars from Alexandria, such as Sosigenes, went to Rome and assisted Caesar with his calendar reforms. But Ptolemy's work is primarily associated with Alexandria and it may have retained some of its past glory. The most likely sites associated with Ptolemy are those of the Musaeum or the Serapeum.
A note on Ptolemy's name. In his Geography there are two places named Ptolemais listed, one in Arsinoites Nome, a naval station, at 61° 40', 29° 20' (Ptolemy's coordinates) just south of Arsinoe at 61° 40', 29° 30' and another Ptolemais Hermiae in Thinites Nome and its major city at 61° 50', 27° 10'. Ptolemy's coordinates list the latitude after the longitude which is measured eastward from the Canary Islands. His longitudes appear to be a little too large. It is believed that Ptolemy was from Upper Egypt.
Friday, April 22, 2011
Thursday, April 21, 2011
Corrected Image for Functions
Wednesday, April 20, 2011
Translating Geocentric to Ecliptic Coordinates
Converting Geocentric Coordinates into Ecliptic Coordinates makes it easier to take into account the precession that takes place over time. In each coordinate frame the principal directions are that of the Equinox, E, the Solstice directions, S and S', and that of the Poles, P and P'. In each frame the direction of the Equinox is the same and we can use primes to indicate the two directions in the Ecliptic frame of reference. The two frames are related by a rotation through the angle of the Inclination of the Ecliptic, ε, about the direction of the Equinox. One can compute these vectors in the Ecliptic frame given those in the Geocentric frame by right multiplying the basis vectors by a rotation matrix and vice versa. To go back to the original basis we do the same but with ε replaced by -ε.
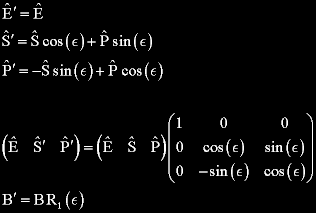
Any direction in the Geocentric frame, e_G, can be found by starting at the Equinox and rotating an angle of α along the equator and then an angle δ towards the pole. The same direction can be found in the Ecliptic frame, e_K, with the angles labeled λ and β. Each representation of the direction can be used to find the components in the Ecliptic frame by repeatedly taking the dot product with one of the principal directions in the Ecliptic frame. The result is a relation between the two sets of angles.
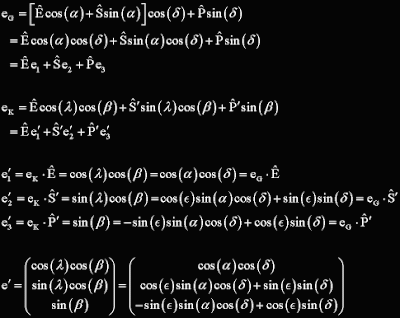
It is easiest to convert from one set of angles to the other if we use the vector representing the direction as an intermediary. The relation between them suggests the use of the following functions.
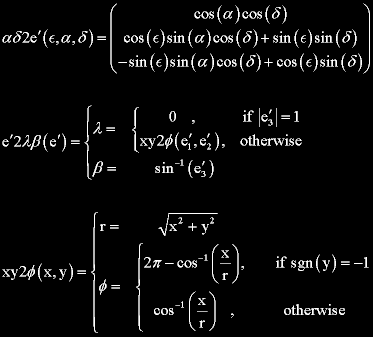
The function "xy2φ" defined above is the equivalent of the "angle" function found in Mathcad. Converting from the direction along the poles is treated separately since both of the components used are zero. The angle λ is indeterminate and is arbitrarily set to zero. Under these circumstances some other condition might be useful in determining λ. Sgn is the sign function*.
Going back to the Geocentric frame after precession in the Ecliptic frame is essentially the same but again one uses -ε instead of ε. Precession is a similar rotation about the Pole of the Ecliptic but only involves adding an angle corresponding to the accumulated precession to the Ecliptic Longitude, λ. The Ecliptic Latitude, β, is unchanged by precession.
*Supplemental: Made a slight change to the definition so xy2φ(1,0) = 0°. Another name for the sign function is signum. The earlier sgn(x) assumed the usual rule for intergers with only negative numbers carring a negative sign. There are older two valued definitions of the sgn function so one has to be careful. The condition y<0 is equivalent to sgn(y)=-1 so sgn(y) is only needed if zero needs special consideration.
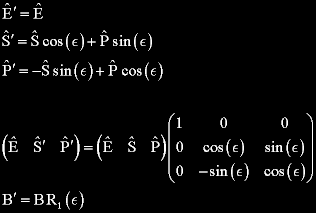
Any direction in the Geocentric frame, e_G, can be found by starting at the Equinox and rotating an angle of α along the equator and then an angle δ towards the pole. The same direction can be found in the Ecliptic frame, e_K, with the angles labeled λ and β. Each representation of the direction can be used to find the components in the Ecliptic frame by repeatedly taking the dot product with one of the principal directions in the Ecliptic frame. The result is a relation between the two sets of angles.
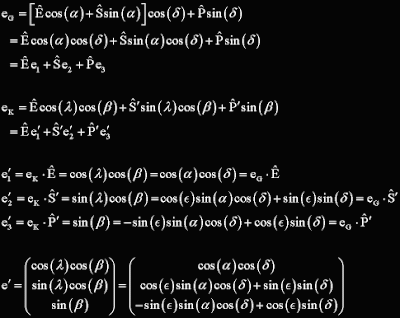
It is easiest to convert from one set of angles to the other if we use the vector representing the direction as an intermediary. The relation between them suggests the use of the following functions.
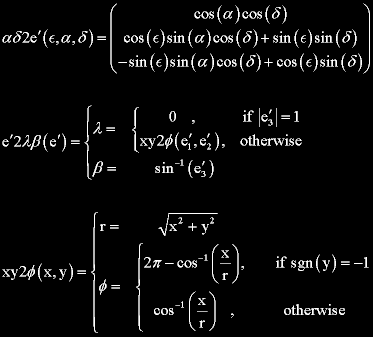
The function "xy2φ" defined above is the equivalent of the "angle" function found in Mathcad. Converting from the direction along the poles is treated separately since both of the components used are zero. The angle λ is indeterminate and is arbitrarily set to zero. Under these circumstances some other condition might be useful in determining λ. Sgn is the sign function*.
Going back to the Geocentric frame after precession in the Ecliptic frame is essentially the same but again one uses -ε instead of ε. Precession is a similar rotation about the Pole of the Ecliptic but only involves adding an angle corresponding to the accumulated precession to the Ecliptic Longitude, λ. The Ecliptic Latitude, β, is unchanged by precession.
*Supplemental: Made a slight change to the definition so xy2φ(1,0) = 0°. Another name for the sign function is signum. The earlier sgn(x) assumed the usual rule for intergers with only negative numbers carring a negative sign. There are older two valued definitions of the sgn function so one has to be careful. The condition y<0 is equivalent to sgn(y)=-1 so sgn(y) is only needed if zero needs special consideration.
Monday, April 18, 2011
The Sky in Ptolemy's Time vs Our Own
Ptolemy points out that there are two primary motions of the heavens. The first is the daily motion associated with the rotation of the Earth. The second is a much, much slower rotation of the Earth's Pole about the Ecliptic Pole with the Vernal Equinox also moving along the Ecliptic at the same time. If we use the order of the Signs of the Zodiac to indicate a direction along the Ecliptic the Equinoxes and the Solstices move slowly in the opposite direction. The Ecliptic Pole is essentially unchanged by this precession.
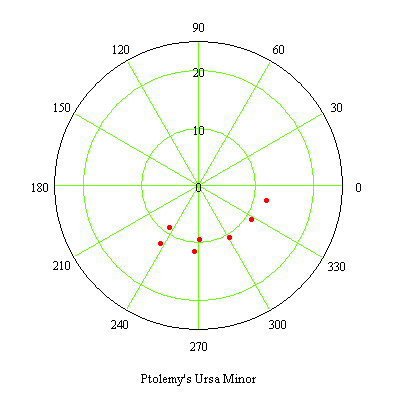
Ptolemy included a catalog of stars in the Almagest and we can compare his sky with the sky as it presently appears. Let's focus on the constellation Ursa Minor which contains the Polaris, the Pole Star. This is shown in the Google Sky view below in which I have marked both the Equatorial and the Ecliptic Poles. You'll probably have to click on it to see it clearly because of its size. The Equatorial Pole is near Polaris and the Ecliptic Pole is in the constellation Draco.

Ptolemy gives the coordinates of the stars in Ursa Minor in Ecliptic Coordinates which complicates the comparison. But the position of these stars can be translated into Geocentric Coordinates using Ptolemy's value for the Inclination of the Ecliptic. From the polar plot below we see that Ptolemy's North Pole was different than ours. In the plot we are looking down on Ptolemy's North Pole in the center so the constellation appears reversed.
In order to determine how much precession has taken place I computed the centers of Ptolemy's Ursa Minor and that of our own in Ecliptic Coordinates and searched for the rotation angle which best matched Ptolemy's constellation with ours.
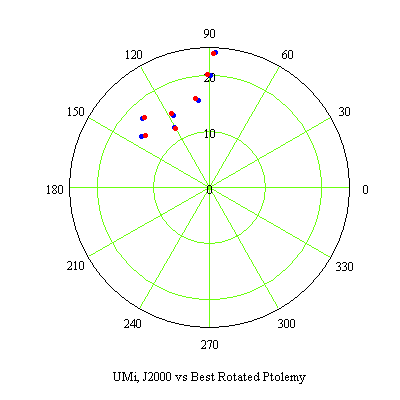
In the image above Ptolemy's Ursa Minor is blue while ours is red. The required rotation was -27.40° along the Ecliptic. This corresponds to an annual precession rate of 53.6"/yr assuming the beginning of 159 AD for the epoch of Ptolemy's sky catalog. The value usually cited for precession is about 50.3" per year.
Ptolemy included a catalog of stars in the Almagest and we can compare his sky with the sky as it presently appears. Let's focus on the constellation Ursa Minor which contains the Polaris, the Pole Star. This is shown in the Google Sky view below in which I have marked both the Equatorial and the Ecliptic Poles. You'll probably have to click on it to see it clearly because of its size. The Equatorial Pole is near Polaris and the Ecliptic Pole is in the constellation Draco.

Ptolemy gives the coordinates of the stars in Ursa Minor in Ecliptic Coordinates which complicates the comparison. But the position of these stars can be translated into Geocentric Coordinates using Ptolemy's value for the Inclination of the Ecliptic. From the polar plot below we see that Ptolemy's North Pole was different than ours. In the plot we are looking down on Ptolemy's North Pole in the center so the constellation appears reversed.

In order to determine how much precession has taken place I computed the centers of Ptolemy's Ursa Minor and that of our own in Ecliptic Coordinates and searched for the rotation angle which best matched Ptolemy's constellation with ours.

In the image above Ptolemy's Ursa Minor is blue while ours is red. The required rotation was -27.40° along the Ecliptic. This corresponds to an annual precession rate of 53.6"/yr assuming the beginning of 159 AD for the epoch of Ptolemy's sky catalog. The value usually cited for precession is about 50.3" per year.
Wednesday, April 13, 2011
Improvement on the Observations of the Sun's Inclination
We know that Ptolemy used averaging to improve the values for the mean motion of the Sun. Making observations of the altitude of the Sun at local noon each day would allow one to directly compare the observations since they are made under similar conditions. The times and position on the horizon of sunrise and sunset vary throughout the year and observations near the horizon also are subject to more atmospheric diffraction. Could Ptolemy have used some sort of averaging to improve on the position of the Sun at the Solstice? When the altitude of the Sun is plotted against the day of year one gets a sinusoidal curve. One needs to know the declination vs right ascension in order to determine the plane of the Sun's apparent motion and determining the right ascension is complicated by the Sun's nonuniform motion along the Ecliptic. Plolemy did determined the Sun's anomaly which measures its deviation from uniform circular motion along the Ecliptic. So he knew both the Sun's altitude and its right ascension.
Plotting these positions on a sphere would show that observations are coplanar or nearly so. Using spherical trigonometry one could estimate the Pole of the Ecliptic from two points on it. How would one improve on the estimate? One could plot the distance of the observations from the equator of the estimated pole and see how linear the fit is using Menelaus' theorem. One knows the right ascension where the Earth's Equator and the Ecliptic cross each other since these points are at the Equinoxes. So only the Inclination of the Ecliptic is unknown.
One would then try to find an Inclination for which the deviation of the Equator of the corresponding Pole would best fit Menelaus' theorem for combinations of three points. Averaging over a number of three point fits would give a better result for the average deviation from the theorem.
One might try a curve fit of this sort to improve on an estimate for the Pole of the Ecliptic. Finding the Inclination for which the sum of the magnitudes of the deviations from an assumed equator is a minimum might also work. Hero of Alexandria showed that the path of light reflecting from a mirror was a minimum. With the right ascensions of the Equinoxes and those for the times of the observations known projecting nearby altitudes of the Sun onto the right ascension of the Solstice and averaging might provide the simplest method for determining the the altitude of the Sun at time of the Solstice. It's easy to do and only involves a little spherical trigonometry. In effect one would be measuring the local zenith or horizon relative to the Ecliptic on a Celestial Sphere with the Ecliptic as the Equator.
Plotting these positions on a sphere would show that observations are coplanar or nearly so. Using spherical trigonometry one could estimate the Pole of the Ecliptic from two points on it. How would one improve on the estimate? One could plot the distance of the observations from the equator of the estimated pole and see how linear the fit is using Menelaus' theorem. One knows the right ascension where the Earth's Equator and the Ecliptic cross each other since these points are at the Equinoxes. So only the Inclination of the Ecliptic is unknown.
One would then try to find an Inclination for which the deviation of the Equator of the corresponding Pole would best fit Menelaus' theorem for combinations of three points. Averaging over a number of three point fits would give a better result for the average deviation from the theorem.
One might try a curve fit of this sort to improve on an estimate for the Pole of the Ecliptic. Finding the Inclination for which the sum of the magnitudes of the deviations from an assumed equator is a minimum might also work. Hero of Alexandria showed that the path of light reflecting from a mirror was a minimum. With the right ascensions of the Equinoxes and those for the times of the observations known projecting nearby altitudes of the Sun onto the right ascension of the Solstice and averaging might provide the simplest method for determining the the altitude of the Sun at time of the Solstice. It's easy to do and only involves a little spherical trigonometry. In effect one would be measuring the local zenith or horizon relative to the Ecliptic on a Celestial Sphere with the Ecliptic as the Equator.
Tuesday, April 12, 2011
The Governing Faculty
Ptolemy says that vision is not just colored light and images but also involves some precessing of what is received by the eye. The power of discernment involves a critical sense which he refers to as the Governing Faculty. Light is a visual flux and colors are related to objects but vision is capable of distinguishing different colors. When looking at a mirror one sees objects in the mirror. There are other optical illusions. The Governing Faculty tries to make sense what is seen [and sometimes fails to do so].
In assessing observations a scientist often needs modify direct measurements to refer them to an observer under standard conditions. The standard observer in astronomy is one in a vacuum at the center of the Earth. Observations are given relative to this reference point to make a comparison of them easier. In a way this is like the Governing Faculty. It forms a common basis for perception.
The closest that Ptolemy comes to discribing the action of a lens is in Bk III, 16 where he describes the shape of the surface of the eye as being like that of a convex mirror while talking about the illusory object in a mirror and its image. The eye or cornea is referred to as the viewer (aspiciens) (see the translation of Ptolemy's Optics by A. Mark Smith) but Ptolemy could just as easily be talking about the Governing Faculty. Ptolemy's model of the eye is that of geometrical optics with off axis rays corresponding to the points of an image. Elsewhere he uses this in reference to the breadth and height of an image and its distance. His model treats images as being three dimensional.
In assessing observations a scientist often needs modify direct measurements to refer them to an observer under standard conditions. The standard observer in astronomy is one in a vacuum at the center of the Earth. Observations are given relative to this reference point to make a comparison of them easier. In a way this is like the Governing Faculty. It forms a common basis for perception.
The closest that Ptolemy comes to discribing the action of a lens is in Bk III, 16 where he describes the shape of the surface of the eye as being like that of a convex mirror while talking about the illusory object in a mirror and its image. The eye or cornea is referred to as the viewer (aspiciens) (see the translation of Ptolemy's Optics by A. Mark Smith) but Ptolemy could just as easily be talking about the Governing Faculty. Ptolemy's model of the eye is that of geometrical optics with off axis rays corresponding to the points of an image. Elsewhere he uses this in reference to the breadth and height of an image and its distance. His model treats images as being three dimensional.
Monday, April 11, 2011
How Well Did Ptolemy Understand Refraction?
Ptolemy does not discuss the simple lens in his Optics. He does have a good understanding of refraction and used a quadrant (Bk V, 7-18) to measure the angles of incidence and refraction at the air/water and air/glass surface. And although he discusses the refraction of simple curved surfaces he does not mention the focusing power of lenses or the creation of images by them. In his Optics, Bk V, 23-30 Ptolemy treats the refraction of the atmosphere as taking place at the boundary between the atmosphere and the aether beyond it. He notes that stars closer to the horizon are refracted more and that the apparent altitude is higher than if no refraction occurred. He also discusses the increase in the apparent size of an object when viewed from a denser medium.
Knowledge of the anatomy of the eye and the action of the crystalline lens does not appear until slightly later in Galen's time. Ptolemy's discussion of visual perception is found in Optics, Bk II. Among the topics he mentions are the eye's optical axis, its cone of perception, stereoscopic vision, the focus of attention and the perception of distance. While Ptolemy talks about object and image there is no discussion of how the eye itself works.
Knowledge of the anatomy of the eye and the action of the crystalline lens does not appear until slightly later in Galen's time. Ptolemy's discussion of visual perception is found in Optics, Bk II. Among the topics he mentions are the eye's optical axis, its cone of perception, stereoscopic vision, the focus of attention and the perception of distance. While Ptolemy talks about object and image there is no discussion of how the eye itself works.
Sunday, April 10, 2011
Effect of Local Environmental Conditions on a Determination of the Inclination of the Ecliptic
To determine the effect of changes in the local environmental conditions on Ptolemy's measurement of the Inclination of the Ecliptic I checked the record of conditions for Alexandria, Egypt at the times of the solstices in 2010 at wunderground.com. The correction factors for Bennet's refraction formula only gave a change of about 1 sec of arc less to the difference in refraction which is rather trivial if one is striving to achieve minute of arc accuracy for the Inclination. Only temperature and pressure corrections were included.
Bessel's Refraction Tables assume more complicated factors for the corrections for temperature and pressure. For more accurate measurements this might make a difference as well as the relative humidity. Since the Earth is not spherical but closer to a rotating ellipsiod changes in latitude might require a correction to the amount of refraction. Nitrogen and oxygen make up 99% of the Earth's atmosphere but that is for a dry atmosphere. Water vapor makes a 1% - 4% contribution near the Earth's surface where the atmosphere is densest and the most refraction occurs. This suggests a simplified model for the Earth's atmosphere.
Is the time of day of a solstice a critical factor? This year the Summer Solstice is at 1716 GMT and the Winter Solstice is at 0530 GMT. So depending on the time zone observations at the exact time of the solstice may not be possible. This year the Summer Solstice is at about 1:16 pm EDT which is a good time for Western Hemisphere including North America and Europe. Weather and timing will probably make the Winter Solstice more difficult to observe directly and one might have to do some sort of curve fit to get a good measurement.
Bessel's Refraction Tables assume more complicated factors for the corrections for temperature and pressure. For more accurate measurements this might make a difference as well as the relative humidity. Since the Earth is not spherical but closer to a rotating ellipsiod changes in latitude might require a correction to the amount of refraction. Nitrogen and oxygen make up 99% of the Earth's atmosphere but that is for a dry atmosphere. Water vapor makes a 1% - 4% contribution near the Earth's surface where the atmosphere is densest and the most refraction occurs. This suggests a simplified model for the Earth's atmosphere.
Is the time of day of a solstice a critical factor? This year the Summer Solstice is at 1716 GMT and the Winter Solstice is at 0530 GMT. So depending on the time zone observations at the exact time of the solstice may not be possible. This year the Summer Solstice is at about 1:16 pm EDT which is a good time for Western Hemisphere including North America and Europe. Weather and timing will probably make the Winter Solstice more difficult to observe directly and one might have to do some sort of curve fit to get a good measurement.
Saturday, April 9, 2011
Effect of Refraction on the Inclination of the Ecliptic
If our goal is to determine the Inclination of the Ecliptic the effect of refraction is not as bad a one might initially believe. One needs to measure the altitude of the Sun on both solstices and each measurement is subject to some refraction. That of the Winter Solstice would have a little more since it is lower in the sky but we take half the difference of the two altitudes to get the Inclination. Since the refractions will be of the same sign they will partially cancel out and only the difference in the refractions contributes to the error in the determination of the Inclination. The effect is more significant at higher latitudes. Ptolemy seems to be aware that a shift in altitude is greater near the horizon than near the zenith (see Toomer p. 421) and shows concern about it in his Optics.
Using 31°, the latitude of Alexandria, in Bennett's formula for the refraction gives a correction of 0° 3' 13.6" if the environmental conditions are unchanged between the Summer and Winter Solstices and along with the correction for vertical deflection it would reduce Ptolemy's Inclination of the Ecliptic to 23° 37' 1.4". Making corrections for changes in altitude from sea level should have a negligible effect on the corrections to the Inclination since they would cancel out on subtraction of the two solstice measurements.
Using 31°, the latitude of Alexandria, in Bennett's formula for the refraction gives a correction of 0° 3' 13.6" if the environmental conditions are unchanged between the Summer and Winter Solstices and along with the correction for vertical deflection it would reduce Ptolemy's Inclination of the Ecliptic to 23° 37' 1.4". Making corrections for changes in altitude from sea level should have a negligible effect on the corrections to the Inclination since they would cancel out on subtraction of the two solstice measurements.
Atmospheric Refraction
The apparent position of the Sun is shifted from its true position by atmospheric refraction so any measurement of its altitude needs to be corrected. The Earth's atmosphere varies in composition, pressure and temperature with height and models such as the standard atmosphere have been created for it.
With these models one can one can compute the curved path of light through the atmosphere by dividing it vertically into thin shells. Bessel's tables were among the most accurate but changes in standards have resulted in their discontinued use. These tables contained the refractions for the standard reference values of pressure and temperature as a function of zenith distance as well as corrections for changes in pressure and temperature near the ground. The relative humidity of the air also contributes some reftaction. These parameters should be recorded at the time of the measurements if later corrections are to be made.
For the altitudes of the Sun at the Solstices in the tropics and middle latitudes the correction for refraction is small and should be less than 3 minutes of arc. One minute of arc along a meridian is a nautical mile.
With these models one can one can compute the curved path of light through the atmosphere by dividing it vertically into thin shells. Bessel's tables were among the most accurate but changes in standards have resulted in their discontinued use. These tables contained the refractions for the standard reference values of pressure and temperature as a function of zenith distance as well as corrections for changes in pressure and temperature near the ground. The relative humidity of the air also contributes some reftaction. These parameters should be recorded at the time of the measurements if later corrections are to be made.
For the altitudes of the Sun at the Solstices in the tropics and middle latitudes the correction for refraction is small and should be less than 3 minutes of arc. One minute of arc along a meridian is a nautical mile.
Friday, April 8, 2011
Summer Solstice 2011
The Summer Solstice this year occurs on Jun 21 at 17:16 UT (GMT). MICA, the Multiyear Interactive Computer Almanac, gives the following data for 2011.


It confirms the time of the Solstice. Note that the Equator and Equinox of Date are used. The Equation of Time is needed to convert standard Daylight Time to local time.


It confirms the time of the Solstice. Note that the Equator and Equinox of Date are used. The Equation of Time is needed to convert standard Daylight Time to local time.
Thursday, April 7, 2011
Measuring the Altitude of the Sun
Ptolemy claims to have used a meridian circle and a quadrant to measure the Inclination of the Sun on the Ecliptic but the shadows produced by a small nail at a distance of 60 cm are rather fuzzy due to the angular width of the Sun. Ptolemy discribes a instrument called a triquetrum (see p. 244 of the Toomer's Almagest), designed to measure the parallax of the Moon, which might be adapted to measure the altitude of the Sun. Replacing the large aperature which was used to sight the Moon with a pinhole and using a screen instead of a small sighting aperature at the other end one can use the triquetrum is reverse. Placing a small lens with a long focal length helps improve the quality of the projected image of the Sun.
It occurred to me that small telescope without an eyepiece could be used as one side of the triquetrum. Using one with a 50mm objective lens with a focal length of 625mm I tested the idea this afternoon. The image produced was quite bright and hot and so I "stopped" the lens down by drawing a circle on an index card slightly larger than the aperature of the telescope at the ojective end and poking a small hole in the card at the center of the circle with the point of the compass. The card was then pressed to fit into the telescope aperature.
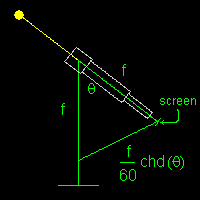
With this arrangement one does not have to wear sunglasses to view the image of the Sun which was focused on a white card and was a little smaller than 1/4 of an inch. As can be seen in the image above two sides of the triquetrum would be equal and form an isosceles triangle. Both the telescope and the measuring rod would pivot on the vertical post. The length of the measuring rod at the bottom between the pivot and the image of the Sun is proportional to the chord of the angle at the top of the triangle.
It would be interesting to see if one could get measurements with this device which are as good as Ptolemy's for the Ecliptic.
It occurred to me that small telescope without an eyepiece could be used as one side of the triquetrum. Using one with a 50mm objective lens with a focal length of 625mm I tested the idea this afternoon. The image produced was quite bright and hot and so I "stopped" the lens down by drawing a circle on an index card slightly larger than the aperature of the telescope at the ojective end and poking a small hole in the card at the center of the circle with the point of the compass. The card was then pressed to fit into the telescope aperature.

With this arrangement one does not have to wear sunglasses to view the image of the Sun which was focused on a white card and was a little smaller than 1/4 of an inch. As can be seen in the image above two sides of the triquetrum would be equal and form an isosceles triangle. Both the telescope and the measuring rod would pivot on the vertical post. The length of the measuring rod at the bottom between the pivot and the image of the Sun is proportional to the chord of the angle at the top of the triangle.
It would be interesting to see if one could get measurements with this device which are as good as Ptolemy's for the Ecliptic.
Tuesday, April 5, 2011
Precession of the Equinoxes
Ptolemy and Hipparchus before him estimated* that the time between the vernal equinox of one year and that of the next was differed from 365 1/4 days by one day in 300 years. This shift has now been more accurately measured over a longer period of time* and is the reason why we skip a leap day* every 400 years. Since the Equinox is defined as the point where the Ecliptic crosses the Equator the direction of the Earth's axis of rotation changes slightly each year. This change is known as precession. The effect is that the direction of the Earth's rotational axis slowly circles the pole of the Ecliptic at the angular distance of the Inclination of the Ecliptic with a period of about 26,000 years. The effect is due to the gravitational attraction on the nonspherical cross section of the Earth caused by the Moon, Sun and the planets.
The significance of this change on global warming can be seen by what happen when the Earth is at perihelion and at aphelion. Currently perihelion occurs on about Jan 3 each year and aphelion is on about Jul 4 and the Earth is closer to the Sun in winter that it is in summer. But the date of perihelion and aphelion do not change with the date of the Equinox. The northern hemisphere of the Earth gets slightly more warming during winter with this orientation than it does when the pole is pointed away from the Sun. The opposite is true for summers. The difference between the amount of sunlight received by a point on the Earth directly beneath the Sun at perihelion and at aphelion is abou 6.7% and while this may not change the average heating of the Earth for the year it will probably affect the extremes in temperature*.
*Edit (5 Apr): changes made to text
The significance of this change on global warming can be seen by what happen when the Earth is at perihelion and at aphelion. Currently perihelion occurs on about Jan 3 each year and aphelion is on about Jul 4 and the Earth is closer to the Sun in winter that it is in summer. But the date of perihelion and aphelion do not change with the date of the Equinox. The northern hemisphere of the Earth gets slightly more warming during winter with this orientation than it does when the pole is pointed away from the Sun. The opposite is true for summers. The difference between the amount of sunlight received by a point on the Earth directly beneath the Sun at perihelion and at aphelion is abou 6.7% and while this may not change the average heating of the Earth for the year it will probably affect the extremes in temperature*.
*Edit (5 Apr): changes made to text
What Should We Consider Minutiae?
Anyone trained in a scientific discipline is taught that some details are relatively unimportant and can be ignored. For example in the study of calculus a differential can be ignored in computing a derivative and some integrals are equal to zero. Similarly in statistics random errors often cancel themselves out when summed. These quantities have little effect when considering the whole but there are small changes that do have a larger effect. A good example would be the effect of summing the squares of quantities which, since all terms are positive, do not cancel themselves out. Quantities like this can contribute to long term changes over time. The contributions that have little or no effect can be considered minutiae. The second set of quantities, however, cannot be ignored and are relevant to the "big picture."
Do We Need Minute of Arc Precision?
We've noticed that uniform circular motion and a spherical shape for the Earth work well as a first approximation. But as one gets more precise in one's measurements one notices smaller changes such as small changes in the length of the day over the year and the effect of the flattening of the Earth. Vertical deflection affects the determination of one's position to one minute of arc accuracy. To measure changes over long periods of time high precision is not necessary. But for the measurement of rapid changes over short periods of time more precise measurements are. So the answer to the question of whether or not we need high precision depends what we are doing.
In the case of global warming changes are more noticable over long periods of time. Currently we are concerned about the effect of greenhouse gases on our environment and we need accuracy to fractions of a degree in temperature to measure this. If we are to be consistent we also need to take into consideration the small changes of other effects over time in order to get a better picture of what is happening.
One also needs to take into consideration the level of education one is working at. For the high school and elementary levels high precision is not necessary for the introductions of our classes. But at the university level one expects more expertise and a more detailed discussion is necessary. Context is important.
So, does the general public need to concern itself with minutiae?
In the case of global warming changes are more noticable over long periods of time. Currently we are concerned about the effect of greenhouse gases on our environment and we need accuracy to fractions of a degree in temperature to measure this. If we are to be consistent we also need to take into consideration the small changes of other effects over time in order to get a better picture of what is happening.
One also needs to take into consideration the level of education one is working at. For the high school and elementary levels high precision is not necessary for the introductions of our classes. But at the university level one expects more expertise and a more detailed discussion is necessary. Context is important.
So, does the general public need to concern itself with minutiae?
Monday, April 4, 2011
Geodetic vs Geocentric Latitudes
The latitude used for maps and GPS is also known as the geodetic latitude. It is very close in value to the geocentric latitude and its deviation from that value is the vertical deflection. Ptolemy was not familiar with the ellipsoid shape of the Earth's surface and the latitudes he uses reflect this. In his Geography Ptolemy lists the latitude of Alexandria as being 31°. If we add the vertical deflection to this we get the modern geodetic latitude for Alexandria is about 31° 11'. In the Greek text of Ptolemy's Geography one finds common fractions used to represent angles less than a degree. The smallest fraction used is 1/12 of a degree which is 5 minutes of arc. Round off errors would again be about 2' 30". Since Ptolemy's Inclination was off by the vertical deflection his latitudes are probably geocentric latitudes.
I found a formula for calculating the Obliquity of the Ecliptic, the modern term used for the Inclination of the Ecliptic, in the Explanatory Supplement to the Astronomical Almansc (p. 171). The Almagest was probably written between 150 AD and 168 AD, the time if Ptolemy's death. Using the beginning of 159 AD as a nominal date the formula gives an inclination of 23° 40' 32.5" which is close to Ptolemy's value corrected for the vertical deflection.
If Ptolemy's angular scale was only accurate to 1/12th of a degree, how could he get a value for of the Inclination of the Ecliptic accurate to 1/3 of a minute of arc? What may have happened is that he measured the difference between the values of the Sun's declination at the Summer and Winter Solstices over a number of years and averaged the results which would give an improved estimate. If his scale indicated twelveths of a degree it would be possible for him to estimate an angle to an accuracy of 1/24th of a degree. This would mean that his measurements were then accurate to at most 2 minutes of arc. While his estimates of the inclination may have approached an accuracy of one minute of arc, his practice seems to have been to do calculations to the second sexagesimal place in order to minimize round off errors.
I found a formula for calculating the Obliquity of the Ecliptic, the modern term used for the Inclination of the Ecliptic, in the Explanatory Supplement to the Astronomical Almansc (p. 171). The Almagest was probably written between 150 AD and 168 AD, the time if Ptolemy's death. Using the beginning of 159 AD as a nominal date the formula gives an inclination of 23° 40' 32.5" which is close to Ptolemy's value corrected for the vertical deflection.
If Ptolemy's angular scale was only accurate to 1/12th of a degree, how could he get a value for of the Inclination of the Ecliptic accurate to 1/3 of a minute of arc? What may have happened is that he measured the difference between the values of the Sun's declination at the Summer and Winter Solstices over a number of years and averaged the results which would give an improved estimate. If his scale indicated twelveths of a degree it would be possible for him to estimate an angle to an accuracy of 1/24th of a degree. This would mean that his measurements were then accurate to at most 2 minutes of arc. While his estimates of the inclination may have approached an accuracy of one minute of arc, his practice seems to have been to do calculations to the second sexagesimal place in order to minimize round off errors.
Ptolemy's Inclination of the Ecliptic
One can find a table for the Ptolemy's Inclination of the Ecliptic, the path of the Sun, in Toomer's Almagest on page 72. In Ptolemy's time the Sun was treated like the planets and so its inclination is given relative to the Earth's equatorial plane. The table is a function of the Sun's declination, δ, versus its ecliptic longitude, λ. It is computed to two sexagesimal places and agrees very well with the function λ2δ for the transformation of a point on the Ecliptic to Equatorial coordinates shown below with the inclination, i = 23° 51' 20". The other function, λ2α gives the angle, α, of the projection of a point on the ecliptic onto the equatorial plane. Both the ecliptic longitude and the equatorial angle are measured from the point where the two planes intersect at the point which defines the Spring Equinox.
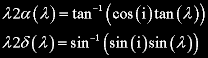
If one converts these inclinations of the Sun to sexagesimals and compares them with Ptolemy's values one finds that the magnitude of the difference, mag_ΔDecl, is only a few seconds of arc. Some of the larger differences can be attributed to transcription errors and those below about 3 seconds of arc may be due to round off errors which occurred during the process of calculation. mag_ΔDecl was multiplied by 3600 to convert from the difference in degrees to seconds.

Ptolemy's value for the inclination of 23° 51' 20" seems a bit too large when compared with the modern value of 23° 26' 21.4" but Ptolemy probably assumed a spherical Earth. If one takes into account the vertical deflection of the plumb bob that he used to determine vertical due to an ellipsoidal surface for the Earth one gets a slightly better value for the declination. Subtracting a vertical deflection of 0° 11' 5" for Alexandria's latitude of 31° 11' 0" one gets an inclination of 23° 40' 15". Ptolemy may have only measured angles to 1/12 of a degree and the round off error of 1/24th degree corresponds to an error of 0° 2' 30". So the unaccounted difference between Ptolemy's inclination and the modern value may only amount to 10' to 13'. The Earth's precession does not change the angle between its axis of rotation and the plane of the ecliptic but nutation introduces some small changes.
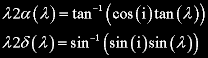
If one converts these inclinations of the Sun to sexagesimals and compares them with Ptolemy's values one finds that the magnitude of the difference, mag_ΔDecl, is only a few seconds of arc. Some of the larger differences can be attributed to transcription errors and those below about 3 seconds of arc may be due to round off errors which occurred during the process of calculation. mag_ΔDecl was multiplied by 3600 to convert from the difference in degrees to seconds.

Ptolemy's value for the inclination of 23° 51' 20" seems a bit too large when compared with the modern value of 23° 26' 21.4" but Ptolemy probably assumed a spherical Earth. If one takes into account the vertical deflection of the plumb bob that he used to determine vertical due to an ellipsoidal surface for the Earth one gets a slightly better value for the declination. Subtracting a vertical deflection of 0° 11' 5" for Alexandria's latitude of 31° 11' 0" one gets an inclination of 23° 40' 15". Ptolemy may have only measured angles to 1/12 of a degree and the round off error of 1/24th degree corresponds to an error of 0° 2' 30". So the unaccounted difference between Ptolemy's inclination and the modern value may only amount to 10' to 13'. The Earth's precession does not change the angle between its axis of rotation and the plane of the ecliptic but nutation introduces some small changes.
Saturday, April 2, 2011
Two History of Astronomy Books
Here are a couple of good surveys on the history of astronomy.
A History of Astronomy - A. Pannekoek
Aristarchus of Samos - Sir Thomas Heath
The first is a general history which ranges from ancient to modern times. The second contains a reprint of Aristarchus's work on the diameters and distances of the Sun and the Moon as well as some coverage of prior efforts in Greek astronomy.
A History of Astronomy - A. Pannekoek
Aristarchus of Samos - Sir Thomas Heath
The first is a general history which ranges from ancient to modern times. The second contains a reprint of Aristarchus's work on the diameters and distances of the Sun and the Moon as well as some coverage of prior efforts in Greek astronomy.
Subscribe to:
Posts (Atom)
