The Sky in Ptolemy's Time vs Our Own

Ptolemy points out that there are two primary motions of the heavens. The first is the daily motion associated with the rotation of the Earth. The second is a much, much slower rotation of the Earth's Pole about the Ecliptic Pole with the Vernal Equinox also moving along the Ecliptic at the same time. If we use the order of the Signs of the Zodiac to indicate a direction along the Ecliptic the Equinoxes and the Solstices move slowly in the opposite direction. The Ecliptic Pole is essentially unchanged by this precession.

Ptolemy included a catalog of stars in the Almagest and we can compare his sky with the sky as it presently appears. Let's focus on the constellation Ursa Minor which contains the Polaris, the Pole Star. This is shown in the Google Sky view below in which I have marked both the Equatorial and the Ecliptic Poles. You'll probably have to click on it to see it clearly because of its size. The Equatorial Pole is near Polaris and the Ecliptic Pole is in the constellation Draco.


Ptolemy gives the coordinates of the stars in Ursa Minor in Ecliptic Coordinates which complicates the comparison. But the position of these stars can be translated into Geocentric Coordinates using Ptolemy's value for the Inclination of the Ecliptic. From the polar plot below we see that Ptolemy's North Pole was different than ours. In the plot we are looking down on Ptolemy's North Pole in the center so the constellation appears reversed.


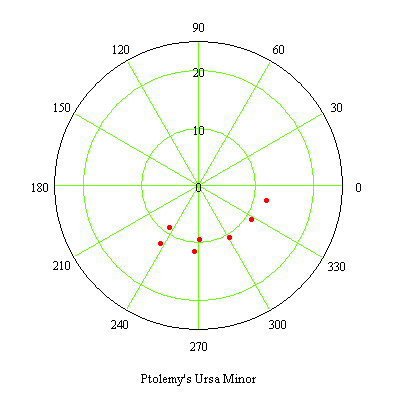
In order to determine how much precession has taken place I computed the centers of Ptolemy's Ursa Minor and that of our own in Ecliptic Coordinates and searched for the rotation angle which best matched Ptolemy's constellation with ours.


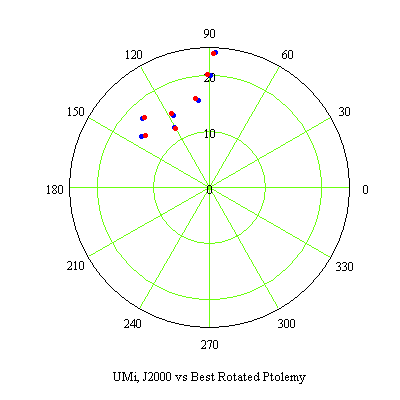
In the image above Ptolemy's Ursa Minor is blue while ours is red. The required rotation was -27.40° along the Ecliptic. This corresponds to an annual precession rate of 53.6"/yr assuming the beginning of 159 AD for the epoch of Ptolemy's sky catalog. The value usually cited for precession is about 50.3" per year.