Ptolemy's Inclination of the Ecliptic

One can find a table for the Ptolemy's Inclination of the Ecliptic, the path of the Sun, in Toomer's Almagest on page 72. In Ptolemy's time the Sun was treated like the planets and so its inclination is given relative to the Earth's equatorial plane. The table is a function of the Sun's declination, δ, versus its ecliptic longitude, λ. It is computed to two sexagesimal places and agrees very well with the function λ2δ for the transformation of a point on the Ecliptic to Equatorial coordinates shown below with the inclination, i = 23° 51' 20". The other function, λ2α gives the angle, α, of the projection of a point on the ecliptic onto the equatorial plane. Both the ecliptic longitude and the equatorial angle are measured from the point where the two planes intersect at the point which defines the Spring Equinox.


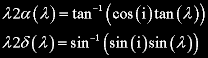
If one converts these inclinations of the Sun to sexagesimals and compares them with Ptolemy's values one finds that the magnitude of the difference, mag_ΔDecl, is only a few seconds of arc. Some of the larger differences can be attributed to transcription errors and those below about 3 seconds of arc may be due to round off errors which occurred during the process of calculation. mag_ΔDecl was multiplied by 3600 to convert from the difference in degrees to seconds.


Ptolemy's value for the inclination of 23° 51' 20" seems a bit too large when compared with the modern value of 23° 26' 21.4" but Ptolemy probably assumed a spherical Earth. If one takes into account the vertical deflection of the plumb bob that he used to determine vertical due to an ellipsoidal surface for the Earth one gets a slightly better value for the declination. Subtracting a vertical deflection of 0° 11' 5" for Alexandria's latitude of 31° 11' 0" one gets an inclination of 23° 40' 15". Ptolemy may have only measured angles to 1/12 of a degree and the round off error of 1/24th degree corresponds to an error of 0° 2' 30". So the unaccounted difference between Ptolemy's inclination and the modern value may only amount to 10' to 13'. The Earth's precession does not change the angle between its axis of rotation and the plane of the ecliptic but nutation introduces some small changes.