The Relative Illuminance of Inscribed Polygons

One can compute the functions for the projected images of the Sun produced by light passing through known apertures. For the case of regular polygons (n-gons) some of the equations needed in Mathcad are shown in the image below. One can start by defining a point, p, in the image plane. The vertices of the n-gon aperture are designated by letter "a" and a point within the aperture is given by q. Δq' gives the distance of the projected image of q in the image plane onto an illuminating disk which represents the Sun. The integral, I, computes the sum of all the flux tubes illuminating a given spot on the screen. A''dλdμ is an element of area in the aperature and to see if its projection from the point on the screen contributes to the sum we have to add the condition that it be within an angular distance θ_S, the Sun's angular radius, from the center of the disk. Using a logic function is convenient since it is either 1 or 0 depending on whether or not the projected point contributes.


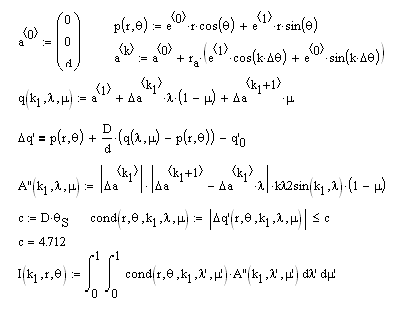
To simplify form of I(r,θ) the n-gon was divided up into n-1 triangles designated by k₁. The entire area of the polygon is the sum, Σ, of n-1 such integrals. This allows one to compute a set of radial curves for various values of θ. One such set for an inscribed triangle is shown below with θ varying from 0° to 90°. The curves are constant when the projection is near the center of the disk but as one crosses its edges fewer points contribute and the curve is sloped as a result. As the number of sides in the aperture increases the resulting curves converge to those of a the circle.


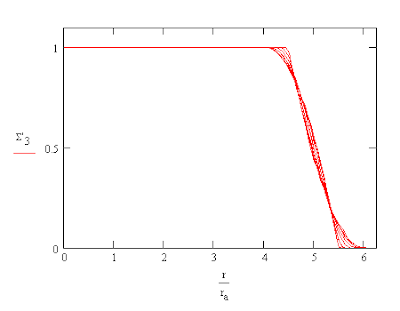
One can also compare the illumination from a number of n-gons inscribed in a circle of radius r_a. In each case the integral for the aperture was divided by the area of the circle which is also found in the formula for the area of the inscribed n-gon, A_n.


The maximum heights of the n-gon integral curves are in agreement with sin(Δθ_n)/Δθ_n. The total area under each of the integral curves is that of the n-gon used for the aperture. Note also that the width of the sloping sides of the illuminated image is equal to the width of the aperture or, in other words, the width of a "line."