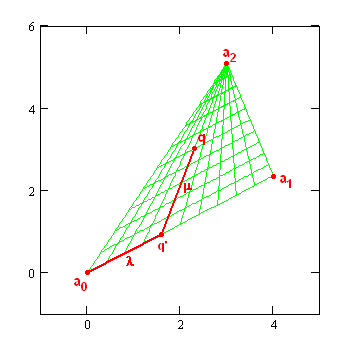
The coordinates used for a position in the aperture for the Sun image calculations are not readily found so it might be good to say a few words about them. I think of them as "triangular" coordinates and they are related to
barycentric coordinates. They are defined with respect to the vertices of a triangle,
ak, as illustrated in the image below. One starts projecting the position of an arbitrary point,
q, from point the
a2 onto the line connecting the first two points meeting it at
q'.
λ is then the fraction of the distance that
q' makes from
a0 to
a1. Similarly
μ is the fraction of the distance that
q makes from
q' to
a2. So both
λ and
μ vary from 0 to 1.
The properties of triangular coordinates are rather interesting. They are fairly easily transformed back and forth from ordinary Cartesian coordinates.

The fundamental forms for the line element and area are not very complicated.

Also the distance between two triangular coordinates can be computed exactly using finite differences.

One can also extend the system to triangular pyramids as can be seen by the projection of a line from an image point through an aperture point. The projection of an arbitrary point in the pyramid onto a plane is unique as is the projection of a point onto a line.




No comments:
Post a Comment